Pronóstico de rendimientos en la bolsa de valores
Aplicación de procesos Poisson-Gaussianos a los rendimientos de los activos en el NYSE: desechando la distribución normal.
Dr. Einar Moreno Quezada
Después de más de 200 años del nacimiento del mercado de valores en la ciudad de Nueva York, EEUU (1792), los inversionistas siguen buscando la mejor manera de poder predecir el comportamiento de los rendimientos de los activos para maximizar sus ganancias. Bachelier (1900) incorporó al movimiento Browniano como un elemento que, siendo aleatorio, nos ayudaría a modelar mejor el comportamiento de las series de tiempo de los rendimientos. Desafortunadamente, las desventajas al incorporar el Browniano incluyen primero, suponer que los rendimientos de las acciones se comportan como log normales y segundo la subvaluación de derivados sobre los precios de los mismos activos. Ante esto, se propuso el uso de una modelación distinta a la que sólo incluye la distribución normal, incorporando “saltos” a través de procesos Poisson, utilizando un trabajo de Sanjiv Das (1998) originalmente aplicado a las tasas de interés. En esta aproximación, desafortunadamente para Das, pero afortunadamente para nuestros fines, la solución de la ecuación diferencial arrojó valores negativos por lo que, dado que el mercado no ofrece tasas de interés negativas, el modelo no prosperó. Así, se utilizaron los rendimientos de los precios de los activos que sí pueden tener comportamientos negativos y positivos. Pero, ¿por qué es importante incorporar procesos de Poisson para modelar el comportamiento de las series de tiempo financieras? El incorporar este tipo de procesos nos abre la posibilidad de modelar “saltos” en el comportamiento de las series. Los saltos en los precios de las acciones son resultado de factores exógenos y bloques de información que hacen que las preferencias y decisiones de los inversionistas sobre la compra-venta de acciones se modifiquen radicalmente en un periodo corto de tiempo. Trabajos previos ya dan evidencia de que es importante modelar los saltos en la Bolsa Mexicana de Valores (BMV). Dado que la BMV pertenece a una economía emergente quedaba pendiente revisar la incorporación de saltos en un mercado de valores perteneciente a un país desarrollado. Así, para esta investigación se utilizaron once activos del New York Stock Exchange (NYSE) y sus series del 1 de enero de 1994 al 31 de diciembre de 2004. La hipótesis nula se define como que los rendimientos de los activos seleccionados ajustan a modelos Poisson-Gaussianos o a modelos ARCH Poisson Gaussianos con un 95% de confianza. La hipótesis alternativa es que los rendimientos de los activos seleccionados ajustan a un modelo ARCH Gaussiano puro. Observemos de inicio el comportamiento de los primeros cuatro momentos de las series de rendimientos.
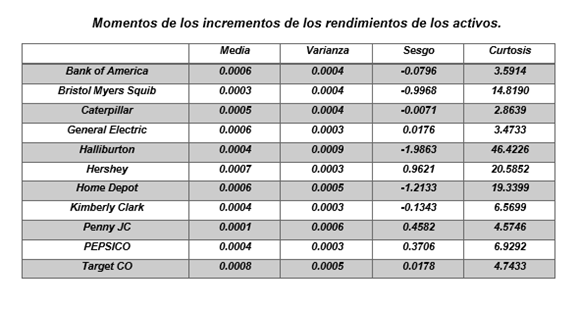
Se puede observar la presencia de sesgo en las series además de activos presentan valores que superan considerablemente los valores de curtosis característicos de una distribución normal.
Al realizar las pruebas con los distintos modelos se obtuvo que de los 11 activos estudiados, 9 aceptaron la hipótesis nula de la siguiente manera:
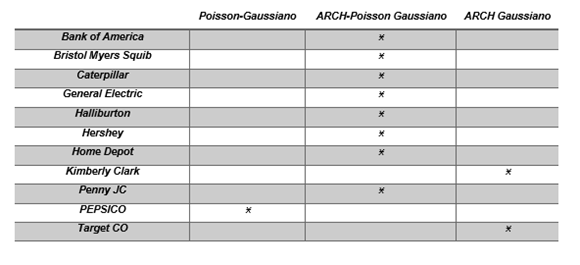
Por lo anterior, se acepta la hipótesis nula en un 81.81% de los casos. Se puede decir entonces que los modelos Poisson-Gaussianos y ARCH Poisson Gaussianos ciertamente funcionan para describir mejor las series de activos que pertenecen al NYSE.
Como se mencionó previamente, la presente investigación está en búsqueda de evidencia para dar continuidad al trabajo de Moreno (2008) y determinar si las conclusiones presentadas en dicho trabajo son exclusivas del mercado mexicano o se replican en economías desarrolladas. Ahora se tiene evidencia que indica que los modelos con saltos ajustan mejor a nuestros datos, hecho que nos motiva a seguir trabajando en esta investigación. Será relevante demostrar paulatinamente el cumplimiento de la hipótesis nula en distintos mercados de valores del continente americano y del mundo. El objetivo es acercarnos cada vez más a la construcción de una teoría financiera que considere las características propias de las series de tiempo financieras.
Este trabajo se encuentra publicado en su versión completa en la Revista Mexicana de Economía y Finanzas Volúmen 10, Número 2, 2015.
