Self-balancing of the disk on an elastic shaft
Journal of Sound and Vibration, 359(2015), pp. 2–20, DOI: 10.1016/jsv.2015.06.035
T. Majewski (UDLAP), D. Szwedowicz (CENIDET Cuernavaca), M. Meraz (Instituto Tecnológico de Puebla)
The paper presents an analysis of the automatic balancing of a rigid disk mounted on an elastic shaft. The balancing system consists of two drums at a variable distance from the disk and free balls (or rollers) inside the disk. The balls are able to change positions with respect to the rotor and compensate for rotor unbalance. This paper presents the equations of motion for the disk as well as for the balls during balancing. It is shown that the balls can compensate a part or all of the rotor unbalance depending on the positioning of the drums. There are vibratory forces that push the balls to new positions; these are responsible for the behavior of the balls and the final results. The vibratory forces are defined as a function of the system´s parameters and they determine the position of equilibrium of the balls. The stability and efficiency of the method is analyzed in this paper.
The balancing system consists of disk 1 with the mass M, two drums 2 and 6, free elements (balls or rollers) 3 and 4, the elastic shaft 5, and the bearings at the ends of the shaft 1 and 8–Fig.1. The mass center of disk C is at a distance e from the axis of rotation of the rotor, which gives a static unbalance Me. The spin velocity of the disk ω is constant.
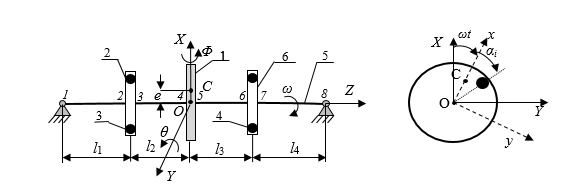
Fig.1. Analyzed system
1-disk, 2-left drum, 3-balls in the left drum, 4-balls in the right drum, 5-shaft, 6-left drum,
1 and 8-bearings
The analysis was done for the system with one or two balls in each drum. To eliminate linear and angular vibrations of the disk, the balls should be able to generate a force and a moment opposite from the excitation. Therefore, the balls should be placed on two planes at some distance from the disk. Using two or more balls on each plane, it was possible to achieve 100% self-balancing of the rigid rotor. The mass of the balls should be selected in accordance with the foreseen maximum unbalance.
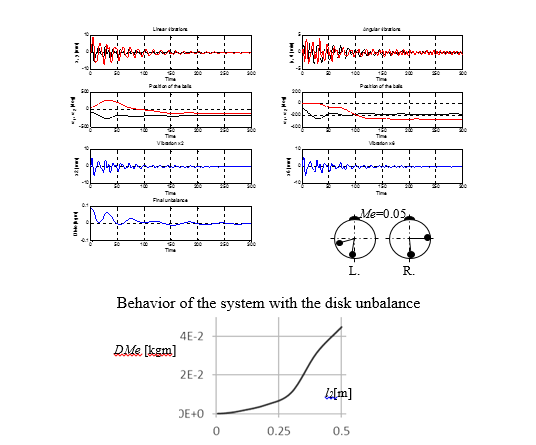
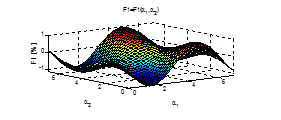
Residual unbalance of the system as a function of the position of the drums
The vibratory forces Fi are functions of the disk unbalance, the position of all the balls, and time. The vibratory forces and depend on the disk vibrations x4(t), y4(t), Φ4(t), θ4(t), and the centrifugal forces from the balls in both drums. Each vibratory force has six components and can be written as
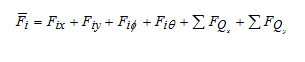
As a result of vibration there are inertial forces that act on free elements (balls, rollers) and change their positions with respect to the rotor. The vibratory forces move the balls to the positions in which they begin to eliminate the vibrations of the shaft on the plane of the balls. Elimination of vibration on one plane does not eliminate vibration on the other plane as they are connected by an elastic shaft.




